Exploring correlation models for repeated measures data analysis: A statistical guide
The VSNi Team
20 October 2021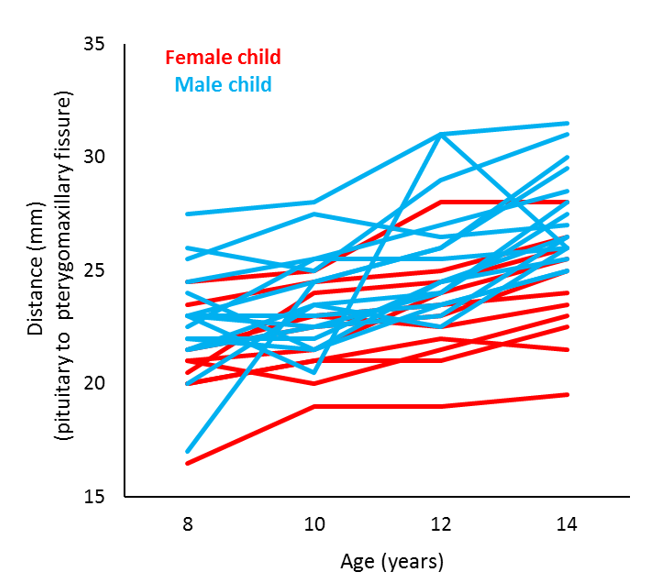
Linear mixed effects models provide a powerful tool for modelling temporally correlated data. The goal of correlation modelling is to describe how the dependence between measurements changes as the separation in time between them increases. For example, if we measure a patient’s blood pressure each month, we expect measurements on consecutive months to be more alike than measurements several months apart.
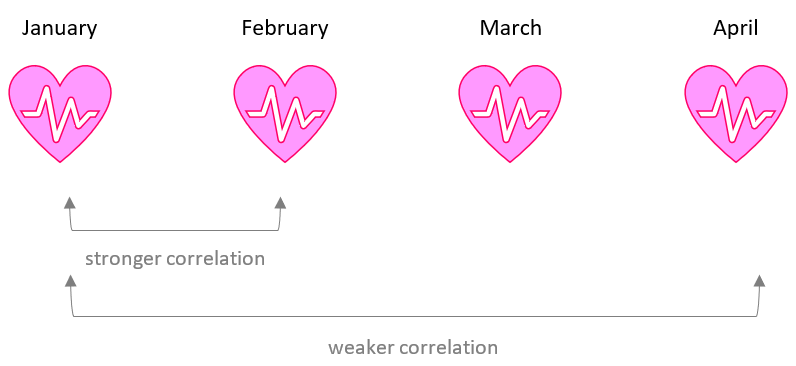
Four commonly used correlation models
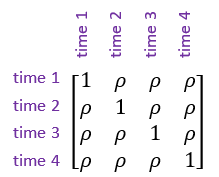
- Simple correlation structure, also known as uniform correlation. This model assumes the correlation () between measurements is constant regardless of how far apart in time they are.
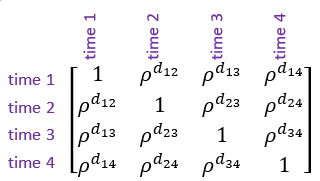
- Autoregressive model of order 1. This model allows the correlations between measurements to decrease as the length of time between them increases. This is a more realistic correlation structure for most repeated measures data sets than assuming constant correlation between all pairs of measurements. However, the autoregressive model should only be used when the repeated measures data is at equally spaced time intervals.

- Power model of order 1. This is an alternative to the autoregressive model of order 1 which accommodates unequally spaced repeated measures. As with the autoregressive model, this allows the correlations between measurements to decrease as the length of time between them increases.
Note: is the Euclidean distance between the and measurements (i.e., time points).
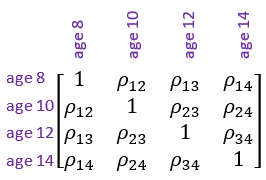
- General correlation structure, also known as unstructured correlation. This is the most flexible correlation structure. It allows a separate correlation for every pair of measurements.

Note: is the Euclidean distance between the and measurements (i.e., time points).
In addition, another important correlation structure is the identity structure. This assumes that the observations are uncorrelated, or independent of one another.
Case study: Orthodontic growth rate study
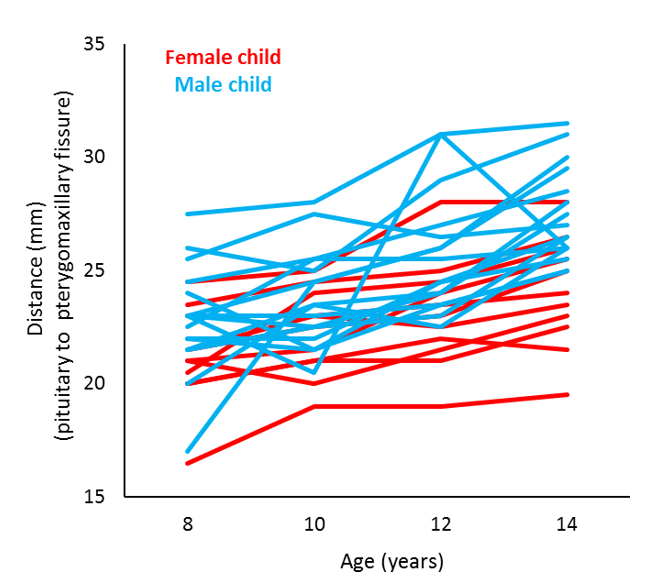
Let’s look at an example. This data is taken from an orthodontic growth rate study of children (Potthoff and Roy, 1964). In this study, researchers at the University of North Carolina Dental School tracked the orthodontic growth of 27 children by measuring the distance between the pituitary and the pterygomaxillary fissure every 2 years from the ages of 8 to 14 years. The graph below plots the orthodontic growth profiles of the individual children, showing the distance data in terms of sex and age.
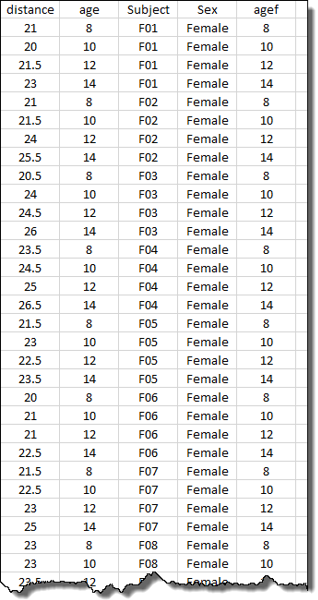
The data set contains 2 variates:
distance, the response variableage, age of the child in years
and 3 factors :
Subject, the individual children from whom repeated measures have been takenSex, sex of the childagef, also age of the child in years but stored as a factor
Incorporating correlation structures in the analysis
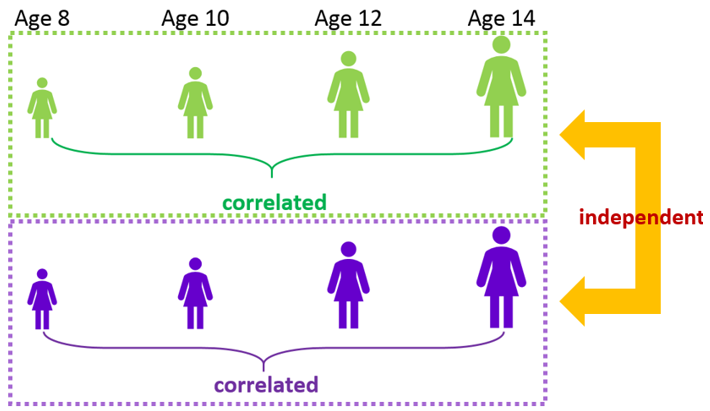
Our goal is to model the distance data allowing male and female children to have different growth patterns as they age. However, as this is repeated measures data, we must take into account the correlated nature of the distance measurements taken on the same child (i.e., Subject) as they age. For this study, distance measurements taken on the same child at consecutive ages should be correlated but measurements on different children are assumed to be independent.
This correlation is imposed by specifying the appropriate correlation structures on the residual.
The orthodontic growth data set contains a total of 108 observations arising from 27 children (factor Subject) each measured 4 times, at ages 8, 10, 12 and 14 (factor agef). Thus, for this data set the residual corresponds to the combination of the factors Subject and agef.
| Our residual model has an I ⊗ C covariance structure, where the identity matrix I corresponds to the independent children, and the covariance matrix C corresponds to the correlated measurements over age within a child. |
Since the distance measurements taken on different children are assumed to be independent, the correlation structure that should be associated with the Subject term in the residual is the identity correlation structure.
However, as the distance measurements taken on the same child over consecutive ages should be correlated, we need to select a different correlation structure for the agef term in the residual.
Recall that:
- the simple correlation structure assumes that the correlation between distance measurements taken on the same child is constant regardless of how far apart in age the measurements were taken
- the autoregressive correlation structure of order 1 and the power model of order 1 allow the correlation between distance measurements taken on the same child to decrease as the age difference between the measurements increase.
- the general correlation structure allows a separate correlation for every pair of ages
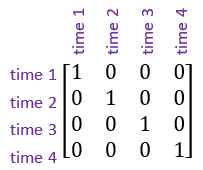
So, for example, if we were to impose a general correlation structure on the agef term in the residual we would be allowing the correlation to be different between every pair ages, i.e.,
Selecting the appropriate correlation structure
In summary, if we model the distance data using a repeated measures model with an identity correlation structure on the Subject term and a general correlation structure on the agef term in the residual, we are saying that the residuals between different children (Subject) are independent, but the residuals originating from measurements taken on the same child but at different levels of agef are correlated according to the general correlation structure.
Popular
Related Reads
